Clustering in Machine Learning

Clustering is a type of unsupervised learning in machine learning where the goal is to group a set of objects in such a way that objects in the same group (or cluster) are more similar to each other than to those in other groups. Clustering is widely used in data mining, pattern recognition, image analysis, information retrieval, and bioinformatics.

What is Clustering?

Clustering involves partitioning a dataset into subsets, or clusters, where data points within each cluster share common traits or characteristics. Unlike supervised learning, clustering does not rely on predefined labels or categories; instead, it discovers these groups based on the inherent structure of the data.

Applications of Clustering

1. Market Segmentation: Identifying distinct groups of customers based on purchasing behavior.
2. Social Network Analysis: Detecting communities within social networks.
3. Image Segmentation: Dividing an image into segments for analysis.
4. Anomaly Detection: Identifying unusual data points that do not fit into any cluster.
5. Document Clustering: Grouping similar documents for topic extraction.

Types of Clustering Methods: 

1. Partitioning Clustering

• K-Means Clustering: Partitions data into K clusters where each data point belongs to the cluster with the nearest mean. It's computationally efficient but requires specifying the number of clusters in advance.
  • Advantages: Simple, scalable, efficient for large datasets.
  • Disadvantages: Sensitive to initial seed selection, requires K as an input, assumes spherical clusters.
• K-Medoids (PAM): Similar to K-Means, but uses actual data points (medoids) instead of means as cluster centers. More robust to noise and outliers.
• Advantages: Less sensitive to outliers than K-Means.
• Disadvantages: More computationally intensive than K-Means.

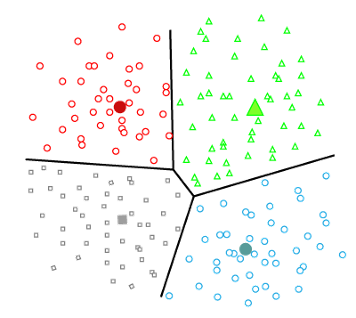Partitioning Clustering

2. Hierarchical Clustering

• Agglomerative (Bottom-Up): Starts with each data point as its own cluster and iteratively merges the closest clusters until only one cluster remains or the desired number of clusters is achieved.
  • Advantages: Does not require specifying the number of clusters in advance, provides a dendrogram for visualization.
  • Disadvantages: Computationally expensive, less efficient for large datasets.
• Divisive (Top-Down): Starts with all data points in one cluster and recursively splits them into smaller clusters.
  • Advantages: Can produce different levels of clustering granularity.
  • Disadvantages: Even more computationally expensive than agglomerative methods.

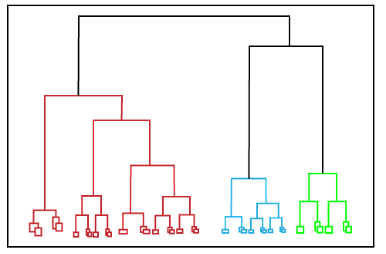Hierarchical Clustering

3. Density-Based Clustering

• DBSCAN (Density-Based Spatial Clustering of Applications with Noise): Forms clusters based on dense regions of data points. It can find arbitrarily shaped clusters and identify noise (outliers).
  • Advantages: Can find arbitrarily shaped clusters, robust to outliers, does not require specifying the number of clusters.
  • Disadvantages: Sensitive to the choice of parameters (epsilon and minPts), may struggle with varying densities.

Density-Based Clustering

4. Model-Based Clustering

• Gaussian Mixture Models (GMM): Assumes that the data is generated from a mixture of several Gaussian distributions. Uses the Expectation-Maximization (EM) algorithm to estimate the parameters.
  • Advantages: Can handle complex cluster shapes, provides a probabilistic assignment of data points to clusters.
  • Disadvantages: Requires specifying the number of clusters, can be computationally expensive.

5. Grid-Based Clustering

• STING (Statistical Information Grid): Divides the data space into a grid and performs clustering within each cell.
  • Advantages: Efficient for large datasets, less sensitive to the input order of data points.
  • Disadvantages: Quality of clustering depends on grid resolution.

6. Fuzzy Clustering

• Fuzzy C-Means: Each data point belongs to all clusters with varying degrees of membership, as opposed to hard assignments in K-Means.
  • Advantages: Provides more nuanced cluster assignments, useful for overlapping clusters.
  • Disadvantages: More complex and computationally intensive, requires specifying the number of clusters and fuzziness parameter.

Choosing the Right Clustering Method

Choosing the appropriate clustering method depends on the specific characteristics of the dataset and the goals of the analysis. Factors to consider include:

• Number of Clusters: Whether the number of clusters is known or needs to be determined.
• Cluster Shape: Whether clusters are expected to be spherical, elongated, or irregularly shaped.
• Noise and Outliers: The presence and importance of handling noise and outliers.
• Scalability: The size of the dataset and computational resources available.
• Interpretability: The need for interpretability and visualization of the clustering results.

Evaluating Clustering Results

Evaluating the quality of clustering results can be challenging since clustering is unsupervised. Common evaluation metrics include:

• Internal Measures: Evaluate the clustering based on the data itself, such as:
• Silhouette Score: Measures how similar a point is to its own cluster compared to other clusters.
• Davies-Bouldin Index: Considers the ratio of within-cluster distances to between-cluster distances.
• External Measures: Compare the clustering results to an external ground truth (if available), such as:
• Adjusted Rand Index (ARI): Measures the similarity between two data clusterings, considering all pairs of samples.
• Normalized Mutual Information (NMI): Measures the amount of shared information between the clustering and the ground truth.
• Visual Inspection: Plotting the data and visually inspecting the clusters can provide insights into their quality.

Clustering is a powerful technique for exploratory data analysis, enabling the discovery of patterns and structures within datasets. By understanding the different types of clustering methods and their applications, you can choose the best approach for your specific data and analysis needs.